安達 直
横波による転覆の危険性ー理論と経験
波浪による転覆の危険性を論じる際、横波は主因の一つとして注目される。以下にその理論と航海経験を照合した。
船体横揺周期：Ts、船幅：BとＧ0Ｍの関係式は、
\(Ts=\dfrac {0.8B}{\sqrt {G_{0}M}} \)・・・①
船体横揺周期：Tsと波浪周期：Twの相互関係は、次の通りとされている。
（１）Ts = Tw ならば、船体横揺が波浪周期と同調する。
（２）Ts > Tw ならば、波面の変化による船体横揺は殆ど無い。
（３）Ts < Tw ならば、波面の変化に追従するような船体横揺が起こる。
パナマ運河可航の最大船型（パナマックス）では、船幅Ｂ=32ｍであり、Ｇ0Ｍ=1mならば、①式からTs=26sとなる。一方、波浪については、「大波浪」と呼ばれる波長：λ=100ｍ、波高：h=10mでもTw=8s程度となる。
波浪周期:Twと波長:λとの関係式は、
\(Tw=\sqrt {\dfrac {2\pi \lambda }{g}}\)・・・②
であり、横揺周期と波浪周期が同調：Ts=26s=Twするには、②式から波長λ≒1000ｍとなり普通に実在しない波浪(津波)となる。従って、パナマックス超の船型が主流の巨大船は（２）Ts>Twの条件を確保しており、横波による転覆はない。
パナマックス型のコンテナ船について
このクラスの船幅は約32ｍであり、大波浪：波長100~150ｍに横たわると、波長の約1/3~1/5を占める。この波浪は周期≒10秒なので船幅を2~3秒で通過する。（人間の最速ランナー程度の伝播速力）
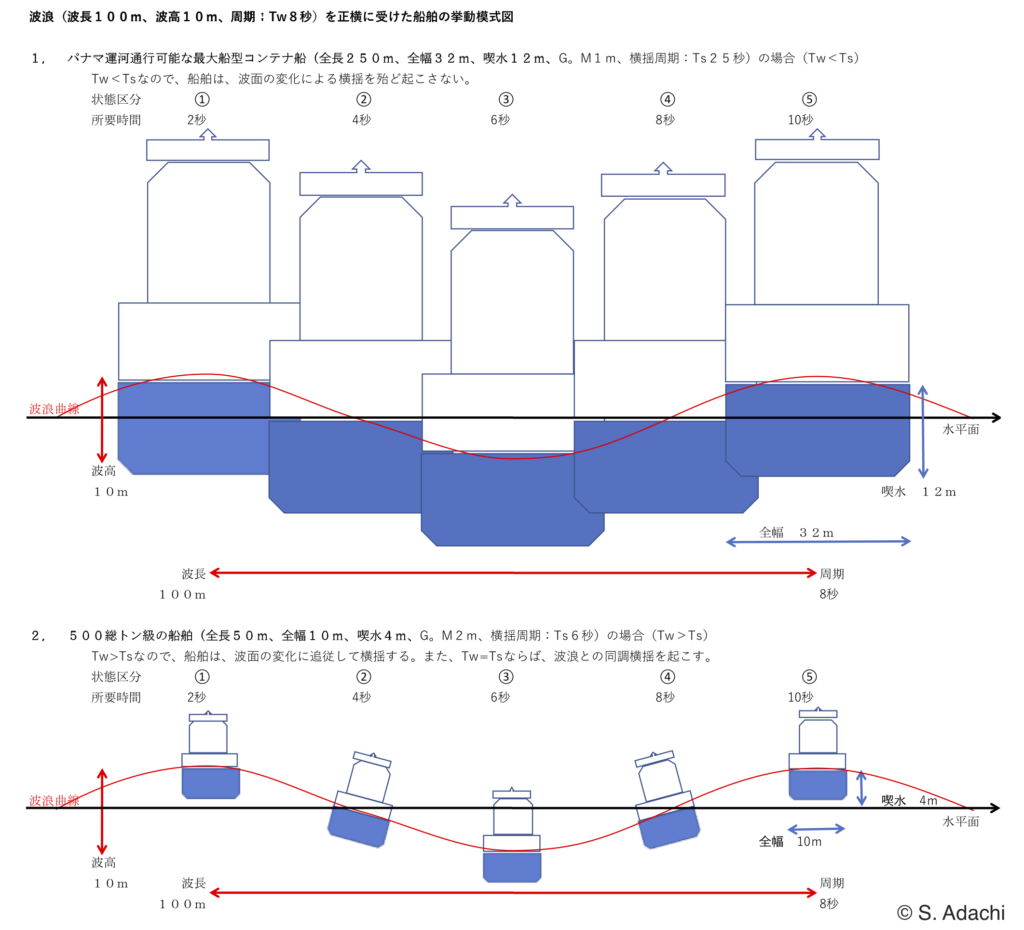
そこで左正横からの波浪による船体横揺運動を船幅毎の間隔で連続的に示すと（下図中の1）の様になる。船舶が波頂に在る時は左右均等な浮力を受けて直立している。次に船体は波頂通過後の右傾斜波面上に移り、船体左右の浮力差で右傾斜を始めようとする。
波浪（波長100ｍ、波高10ｍ、周期：Tw８秒）を正横に受けた船舶の挙動模式図
しかし、波動が船幅を2~3秒で通過するので、船体は右傾斜する間も無く波底に到達してしまう。其処では、浮力が左右均等になり傾斜力は無くなる。或いは、少々惰性で右傾斜しようとしても、瞬間に先程とは逆傾斜の波面上に移っており、右傾斜を戻す浮力を受けながら次の波頂に至る。この間約10秒に対して、本船の自由横揺の往復周期は約25秒であって船体傾斜する間が無く「Ts>Twならば、波面の変化による船体の横揺は軽微」との理論が実際に納得できた。
従って、大型航洋船の波浪との同調は、次の③式が示す通り、横波ではなく斜め追波状態で起こり、両者の出会い周期が同調すればTs＝Tm≒20～25秒となる。
\(Tm=\dfrac{\lambda}{Vw-Vs\cdot \sin \theta}\) ・・・③
θ：波浪との出会い角度（正横方向を0度、真後方向を90度）
例として、船速Vs=10m/s(約20kts)、波長λ=100m、波浪周期Tw=10s、波速Vw=10m/sを上式③に代入すれば、θ=30度：正横より後方30度からの斜め追波と同調する。
パナマックス船型の1／3船幅≒10ｍの船舶について
大波浪（波長λ：100~150ｍ）に横たわると (上図2)の状態となる。また、上記①と②式からTw=\(\sqrt {2\pi 100\sim 150/g}\)≒8~10秒≧Tsとなる。
従って、上記（１）「Ts=Twならば、船体横揺が波浪周期と同調する」と（３）「Ts＜Twならば、波面の変化に追従するような船体横揺が起こる」の条件が当て嵌まる。いずれも「転覆の危険性あり」となるので、このサイズの小型船で「大船に乗った気分」に浸るのは禁物であり、常に波浪を見極めて航行せねばならない。
近年、転覆倒置しても再起する復原力を有するはずの外洋ヨットでさえも、高速化を追求した船型開発に伴う復原性不良での転覆が散見されるので、ロールオーバーしても大丈夫との固定観念の盲信は危険だ。実際の航走では、横揺傾斜しても上甲板が波面を掬わないだけの乾舷高があれば、即ち、凌波性が優れていれば、転覆防止には有利と考えられる。